A Matemática em um game de pegar bolinhas.

Hoje iremos criar um mini-game de caçar bolinhas, o Catchgame (disponível em: ai2.appinventor.mit.edu/?galleryId=5294338782396416), para ser jogado na tela do seu smartphone e observar os conceitos matemáticos envolvidos. Vamos lá?

A ideia do Catchgame é você coletar todas as bolinhas pretas da tela com a bolinha azul (maior), mas sem esbarrar nas vermelhas, pois o jogo reinicia. Cada vez que você coleta as 14 bolinhas pretas você avança um nível (no total são 13 níveis para vencer o game). A cada nível é diminuído meio segundo do total inicial, tornando-se um verdadeiro desafio os últimos níveis, sem contar que as bolinhas sempre são dispostas de modo aleatório. 

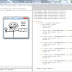
Para inserir o elemento bolinha você deve usar a opção bola dentro de uma pintura, que traça os limites de atuação dessa bola, que ficam no menu de Desenho e Animação (destacados em vermelho). A programação apontada com a flecha azul é responsável por fazer a bolinha Catador (bolinha azul maior) seguir o que o seu dedo toca na tela em posições de X e Y. Olha só o conceito de plano cartesiano aparecendo por aqui.

Indicado com a flecha verde está a programação responsável por fazer a contagem de pontos a cada vez que a bolinha Catador colidir com uma outra bolinha, até o valor máximo de 14 responsável por iniciar o próximo nível. Mas e quando colidir com a bolinha vermelha? Temos destacado com a flecha laranja as três programações responsáveis por isso e que reinicializam o nível.  

Mas e como gerar o posicionamento aleatório das bolinhas na tela? A programação abaixo explica isso. Selecionado em vermelho está a lista de bolinhas a serem distribuídas pela tela, em azul a lei de formação com valores aleatórios entre 30 e o valor máximo da tela de Largura e Altura (destacado em verde) menos os valores 40 e 200 respectivamente, para X e Y e para cada bolinha da lista acima. A flecha em laranja é uma garantia para que as bolinhas sempre estejam visíveis na tela, pois cada vez que uma é catada no game, ela deixa de aparecer até começar novamente um novo nível. Note que para as bolinhas vermelhas será preciso construir uma nova lista e para a bolinha Catador sempre será posicionada em X e Y iguais a zero, que são os valores fora do range randômico das demais, evitando as colisões sem o game estar devidamente iniciado. Aqui o entendimento de como funciona os pontos X e Y em um plano cartesiano se torna essencial.

Finalizando, temos algumas outras funcionalidade que já foram vistas em outras atividades aqui listadas no blog, tais como o uso do TinyDB para elaborar um placar (https://vemfazermatematicaegames.blogspot.com/2018/06/appinventor-2-construindo-um-placar.html) e a construção de um temporizador (https://vemfazermatematicaegames.blogspot.com/2019/01/vamos-desafiar.html). Agora é a sua vez. Como podemos melhorar esse game? Que tal construir fases mais desafiadoras com a possibilidade das bolinhas vermelhas ficarem mudando de local em uma mesma tentativa ou ao tocar as bolinhas vermelhas acabar o game, dentre outras possibilidades. Construa o seu CatchGame e depois venha comentar como foi sua construção e suas percepções sobre o que aprendeu e desenvolveu. Até a próxima!

Construindo um classificador de triângulos.

Que tal o desafio de construir um classificador de triângulos? A principio não parece ser tão complicado, mas e que tal que ele seja randômico na construção do tamanho de lado e de ângulos? Agora sim temos um grande desafio e que vai precisar de bastante Matemática para ser solucionado. No projeto Classificador de Triângulos (https://scratch.mit.edu/projects/289327362/) encontramos a solução para esse desafio.

Vamos começar pela forma de construção de um triângulo qualquer que é a pior situação apresentada. Ao construir um lado, um ângulo e outro lado (esse lado vai funcionar com valores maiores para ser um hipotenusa e dar condição de existência para o triângulo) todos randômicos, temos o mínimo necessário para dar forma ao tipo de triângulo que você quer. 

O problema reside em como fechar esse triângulo! Temos que ter a construção de um segundo ângulo que feche o triângulo, e por isso usamos a função seno (em verde), que com os valores dos lados oposto e da hipotenusa (o segundo lado foi construído propositalmente maior) saberemos o valor do ângulo com exatidão. Mas e a construção do terceiro lado? Simples, só ligar a construção de uma reta até o valor inicial em X e Y do primeiro lado.

Essa foi a construção para o caso do triângulo do tipo escaleno, como dito anteriormente o pior caso de construção. Para o caso do equilátero, teremos a alteração dos valores dos dois primeiros lados sendo exatamente iguais. Para o caso do equilátero, basta fixar o ângulo em 60 graus com valor de 3 lados idênticos (mas construídos com um valor randômico) e podemos usar um aponte para um valor randômico de ângulo para dar diversos posicionamentos ao triângulo equilátero (os demais não necessitam pois tem um valor randômico de construção de ângulo).

Por fim, basta colocar cada um dos tipos de triângulos baseados em classificação de lados em Mais Blocos e colocar dentro da programação inicial acoplando um placar. Que tal agora, construir um classificador de triângulos com base em ângulos (agudo, reto e obtuso)? Ou ainda algum outro tipo de classificação geométrica que não fique restrita apenas a triângulos? Que modificações são necessárias? Deixe nos comentários as suas novas construções e até a próxima!

MathMaker: o seu aplicativo de Matemática para aprender ...

Qualquer conceito matemático!
Se der uma rápida procurada na rede você irá encontrar diversos aplicativos matemáticos, mas, porque procurar um se você pode fazer o seu? Essa é a proposta do MathMaker, o aplicativo que vai ajudar você e seus amigos a aprender Matemática produzindo ele mesmo!
Em primeiro lugar, é importante escolher a temática (conceito, problemas) do game. No caso do MathMaker: Porcentagens (ai2.appinventor.mit.edu/?galleryId=4757974009643008) vai ser apresentado o conceito de porcentagem, alguns exemplos e um game para calcular porcentagens.

As primeiras telas trabalham diretamente com a conceituação e a apresentação de um problema contextualizado na forma de telas que foram produzidas em um editor de imagens, por isso não há grandes desafios, a não ser linkar os botões existentes.

Agora vem a tela (screen) que possui mais desafios de todas as outras: a "Praticando". Nela estão todos os cálculos e opções do game sobre porcentagens. Como podemos ver na imagem abaixo, está destacado com uma flecha (vermelha) os comandos responsáveis por dizer que se a pontuação ficou acima de 10 (que faz o usuário vencer o game) e em amarelo o processo de geração do número aleatório e de percentual aleatório a serem calculados, bem como o processo de cálculo do percentual (ele vai ser comparado com a resposta dada pelo usuário e irá verificar se é verdade ou falsa) e a atualização dos valores na tela. Falando especificamente do calculo percentual, não é algo muito complexo, já que para obter esse valor sempre será o número vezes o percentual divididos por 100 (fração razão 100). Apenas atente-se que foi usado o comando arredondar para ele não destoar dos demais resultados gerados de valores inteiros aleatórios.

O grande desafio ao construir esse aplicativo foi como criar botões de alternativas que mudassem de posição e que as respostas pudessem ser randômicas. Isso foi resolvido (mostrado na imagem abaixo) com a criação da variável global Botão que irá possuir o valor sorteado de 1 a 4 (destacado em vermelho) e, de acordo com o valor (em amarelo), é a posição da resposta correta (obtendo-se o valor calculado acima) e os demais são valores aleatórios entre 1 e 1000.
Ao lado temos que cada botão ao ser clicado faz o teste (em amarelo) verificando se o valor da variável Botão é a que foi sorteada (a exemplo, se Botão vale 1 o botão 2 é o correto e, assim por diante). Caso afirmativo, temos a resposta correta, adicionando-se um valor ao placar (1), atualizando o valor na tela e em seguida reiniciando o processo com um novo calculo percentual. Caso negativo, temos que é a resposta errada, subtrai-se um valor do placar (0,5) e o atualiza na tela e, mantem-se os mesmos valores na tela.

Com isso conseguiu-se estruturar um aplicativo de Matemática que explicou o conceito do que é uma porcentagem, um exemplo e um problema relacionados e aplicou-se um game de cálculos percentuais com placar (gamificação). E isso pode ser aplicado a outros conceitos matemáticos. Que tal testar? Mãos a obra e deixe nos comentários os links dos aplicativos que conseguiu construir. Até a próxima!

Scratch for Games: a gravidade e a força normal em uma simulação.

Quando você programa um game ou uma simulação, algo que é muito pertinente na movimentação de um personagem é a gravidade. Você sabe o que é a gravidade? E a força normal? Talvez tenha se lembrado algo relacionado a conceitos da Física, e sim, esse é o caminho que seguiremos, mais especificamente, vamos construir uma simulação em Scratch que simule a movimentação de uma bola com a ação da gravidade (não a da Terra, uma fictícia) e da força normal. O importante aqui é a Matemática envolvida para fazer o sistema funcionar.

Quando você acessa o projeto Scratch for Games: Gravidade e a Força Normal (https://scratch.mit.edu/projects/216854906/) é possível movimentar uma bola pelo cenário (usando as setas direcionais). Experimente apertar a seta para cima e você vai verificar que é possível "lançar" a bola para o alto e que ela cai lentamente ao soltar a tecla (gravidade agindo). Isso se deve ao fato de ter construído na programação um comando "sempre adicionar um valor -0.9 em y caso não toque o verde (chão)". 

É claro que isso gera um problema da bola cair continuamente e sabemos que existe um chão onde ela deve parar. É aí que entra em ação a força normal que podemos definir como aquela que é feita por uma superfície (em contato) a fim de sustentar um objeto depositado sobre ela, sendo ela sempre perpendicular. Podemos "entender" como uma força de reação a força da gravidade de modo a se anularem. Dito isso, ao observar o comando destacado em vermelho no Scratch, foi colocado dentro do loop "sempre" um "adicione um valor 0.9 em y caso toque o verde (chão)". Com isso, o personagem bola, ao encostar no chão verde passa a anular seus valores no eixo y, tal como a proposição da Física descreve a força normal.

Agora temos um novo desafio, colocar um objeto (pedra) no meio do percurso e tentar programar um modelo para que a bola possa ser deslocada e que caso ela fique em um dos lados da pedra, a bola role para um dos lados dela.

Como podemos ver, dentro do bloco "sempre" temos duas cores cinzas que são os lados da pedra (sim, a pedra não foi desenhada com uma sombra a toa) e cada uma delas, além de ter a o valor em y de 0.9 (que é a normal da pedra em lugar do chão verde), temos os valores em x de 0.5 (direita) e -0.5  (esquerda) que vão fazer a bola deslizar para um dos lados da pedra.

Assim, conseguimos com alguns valores definidos fora dos padrões da realidade (gravidade da Terra que é de 9,8 m/s), construir um sistema físico bem definido (da força normal), criando um simulação das forças atuantes em uma bola de futebol e como ela se comporta ao ser deslocada pelo cenário. Gostou? Que tal fazer outros obstáculos desafiadores ou ainda criar outras simulações físicas? Deixe nos comentários as suas criações e percepções. Até a próxima!