O uso de variáveis no Modelamento Geométrico

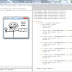
Na Matemática, o conceito de variável é atrelado ao estudo de funções, onde podemos ter um conjunto finito ou não de valores desconhecidos, mas que podem ser atrelados a uma regra de construção. Essa definição é muito importante no modelamento de objetos, pois permite fazer construções de objetos escalonados (que podem ter diversos tamanhos) e que podem sofrer modificações sem alterar as regras básicas de construção.

Como podemos ver acima, logo no início da programação são definidos duas variáveis, "valor1" e "valor2" que são igualadas a valores numéricos, estes inclusive podem ser alterados e a peça irá ter um novo redimensionamento (teste a vontade). Estes dois valores estão presentes dentro da programação de construção (união entre cilindro e cubo rotacionado) e temos que: o "valor1" é referente aos valores X e Y do plano, no qual o cilindro tem o raio e o cubo tem as coordenadas cartesianas X e Y (destacados em verde). Já o "valor2" é referente ao eixo Z, no qual o cilindro tem a altura (h) e o cubo tem a terceira coordenada cartesiana (Z) (destacados em laranja). Desse modo, independente do valor que for colocado nas duas variáveis, a construção irá manter suas regras de proporcionalidade de construção.
É possível ainda fazer operações com as variáveis criadas de modo a manter uma mesma escala na construção total do objeto, como podemos ver no código abaixo:

valor1 = 40; valor2 = valor1*0.9; color ("limegreen") union() { cylinder(r=valor1,h=valor2,center=false); cube(size=[valor1,valor1,valor2],center=false); }

Observe que o comando "valor2 = valor1*0.9" irá construir todos os valores da variável "valor2" com o tamanho escalonado em 0,9 da variável "valor1". Esse tipo de construção irá garantir sempre a proporcionalidade da sua construção como um todo, caso essa seja sua intenção.
Existem outras formas de ajustar suas construções usando os comandos "scale([x,y,z])" e "resize(newsize=[x,y,z])" que são responsáveis por escalonar e redefinir os tamanhos dos sólidos, mas o ponto negativo é que são feitos por sólidos e não de maneira geral como usando as codificações com variáveis:

Finalizando, a importância algébrica na construção de modelos geométricos permite você abstrair melhor outras situações e não ficar na dependência de valores numéricos. A partir de agora é com você. Passe a fazer suas construções em função de variáveis e com o tempo você verá que é muito mais prático. Deixe nos comentários abaixo suas impressões e até a próxima!

OpenSCAD: Como colorir e escrever em objetos

Prototipar objetos também exige um grau de criatividade que perpassa pelo uso de escritas e de cores. Embora no modelamento geométrico a cor utilizada não irá ser necessariamente a utilizada na impressão final (já que depende do filamento usado), ter o objeto colorido na área de construção do OpenSCAD já dá uma boa noção de como ele ficará (uso apenas no virtual). Assim como, a possibilidade de escrita ajuda a estilizar o objeto e deixar ele com a aparência de algo único.

Em primeiro lugar para para colorir um objeto, podemos usar três possibilidades diferentes, todas elas usando a nomenclatura de cores (link SVG Color List: https://www.w3.org/TR/css-color-3/#svg-color):

• Nome por extenso em inglês: usando o comando "color ("nome da cor")" (destacado em vermelho);
• Nomenclatura Hex RGB: usando o comando "color ("nomenclatura HEX RGB")" (destacado em laranja);
• Valor decimal: usando o comando "color ([ R/255, G/255, B/255 ]), onde o R, G, B devem ser substituídos pelos valores decimais de coloração (destacado em azul).

Para escrever textos no OpenSCAD é bem simples. Basta apenas escrever o seguinte código "text ("digite seu texto")". Agora, se você quiser incrementar o seu texto com cores diferentes ou até mover ele de posição, o código abaixo é um exemplo perfeito de como é possível fazer isso:

Todos os códigos aqui utilizados podem ser baixados deste link: https://drive.google.com/drive/folders/1m0nQDvmQA8tD8c1OdPT4Md-YtH7C75t3?usp=sharing. Assim finalizamos esse post e agora é com você. Deixe nos comentários abaixo suas dúvidas e construções usando o OpenSCAD. Até a próxima! 

Projeção de sólidos no OpenSCAD

Podemos entender como uma projeção, a sombra que o sólido geométrico sobre um plano. No OpenSCAD isso é possível usando o comando "projection ()". Veja abaixo duas possibilidades de uso de projeção em um sólido formado pela diferença entre um cubo e uma esfera:

Como podemos ver acima, a sombra formada nas projeções assume duas formas diferentes:

• Projeção de todos os pontos em Z: nesse caso a projeção leva em conta a visão de todos os pontos no eixo Z e funciona como se uma luz projetasse sua sombra do alto do eixo positivo em Z. A programação é dada por:      

projection(cut = false) { difference() { cube(30, center = true); sphere(20); } }

• Projeção somente dos pontos em Z igual a zero: nesse caso é levado em consideração somente o formato do sólido em Z=0 e é realizada a projeção com base nisso. Sua programação é dada por:   

projection(cut = true) { difference() { cube(30, center = true); sphere(20); } }

Nem sempre o sólido está na posição que você quer para obter a projeção, por isso a possibilidade de rotacionar o sólido precisa ser cogitada. Usando o comando "rotate([x,y,z])" onde os valores x,y,z são os ângulos de rotação para o seu sólido, teremos um novo formato de projeção (no caso abaixo foi rotacionado 45 graus no eixo X):

Com isso temos o básico para trabalhar com projeções que são muito importantes na Geometria Descritiva. Agora é a sua vez, comece a construir seus objetos e faça as projeções necessárias, depois deixe nos comentários abaixo as suas impressões. Até a próxima!

Operações boleanas no OpenSCAD: a união, a diferença e a intersecção em sólidos.

Na modelagem 3D existem três tipos principais de operações com sólidos (que no OpenSCAD são denominadas de operações booleanas, se você quiser saber mais pesquise por esse termo na rede): a união, a diferença e a interseção que são totalmente necessárias para você fazer a construção de objetos que se derivem dos sólidos geométricos primitivos. Abaixo, você pode ver as três operações em questão com o uso de dois cilindros (o segundo cilindro sempre está rotacionado em noventa graus):

Para chegar nessas três construções usou-se as seguintes definições e códigos:

• União: operação definida como a soma dos volume dos dois cilindros formando uma figura única e que pode ser obtida pelo seguinte código:

union() { cylinder (h = 4, r=1, center = true, $fn=100); rotate ([90,0,0]) cylinder (h = 4, r=0.9, center = true, $fn=100); }

• Diferença: operação definida como a subtração dos volumes do cilindros, lembrando que nessa operação a ordem de qual objeto é subtraído de outro faz diferença. Recomenda-se testar o código abaixo com a ordem trocada dos códigos dos cilindros para compreender melhor:

difference() { cylinder (h = 4, r=1, center = true, $fn=100); rotate ([90,0,0]) cylinder (h = 4, r=0.9, center = true, $fn=100); }

• Interseção: operação definida com o volume em comum entre os dois cilindros e se desprezando os volumes que não estão em comum:

intersection() { cylinder (h = 4, r=1, center = true, $fn=100); rotate ([90,0,0]) cylinder (h = 4, r=0.9, center = true, $fn=100); }

Como podemos ver acima a estrutura dos códigos é semelhante mudando apenas o nome da operação. Mas e se caso precisássemos combinar mais do que uma dessas operações? Nesse caso precisamos escrever o código na ordem de construção, respeitando a ideia de construção de conjuntos, ou seja, a ordem das chaves é muito importante, veja o exemplo abaixo:

Observando a imagem acima, temos primeiramente a união do cilindro e do paralelepípedo (cube) para criar uma peça única todos dentro de uma unica chave (destacado em vermelho) e, em seguida, é realizada a diferença entre essa peça criada com o cilindro responsável pelo furo (destacado em verde):

difference() { union() { cylinder (h = 4, r=2, center = true, $fn=100); translate ([1.5,-0.5,0]) cube([10,1,2]); } cylinder (h = 4.1, r=1, center = true, $fn=100); }

Por hoje foi isso. Agora você tem as bases mínimas para produzir objetos em 3D que consiste em saber a programação dos sólidos e suas dimensões, como movimentar eles e como fazer operações boleanas. Deixe nos comentários abaixo suas criações e até a próxima!

Extrusão Linear: transformando figuras 2D pro 3D.

Extrusão linear é uma operação de modelagem na qual pega-se um polígono 2D como entrada (eixos X e Y) e o estende na terceira dimensão (eixo Z) obtendo-se uma forma 3D. Na industria tem-se uma aplicação muito grande, podendo dar-se o exemplo a barra de suporte abaixo:

Vamos começar fazendo uma extrusão linear a partir de uma construção 2D, mais precisamente um círculo unido a um paralelogramo e realizado a diferença em relação a um hexágono em seu interior (destacado o código em vermelho). Veja abaixo a diferença entre a construção 2D e a construção 3D após a extrusão linear (lembrando que o código destacado em verde é o responsável por isso): 

Para o exemplo acima foi usado o seguinte código:

linear_extrude(height = 10, center = false, convexity = 5, twist = 0) difference() { union() { circle(r=2, $fn=360); translate ([1.5,0,0]) square([10,1]); } circle(r=1.5, $fn=6); }

Além de estender em Z, a extrusão linear pode criar torções em torno desse eixo para produzir molas, barras roscadas, dentre outras possibilidades. Veja no exemplo abaixo, o que a alteração do valor na opção "twist=250" produz (note que foi retirado a união do exemplo acima para ficar mais simples de ver a torção hexagonal):

Outro exemplo possível, é usando a diferença em dois círculos e a opção de valor "twist=3000" criando uma mola em torno do eixo Z. Note que foi realizado uma translação, pois é exatamente esse distanciamento do eixo que promove esse efeito radial: 

Todos os códigos aqui utilizados podem ser encontrados no seguinte link: https://drive.google.com/drive/folders/1JFNPK373YLqBkcLyCeNMIds4Nvvb-IgP?usp=sharing. Outra dica também é que colocando o sinal de negativo no twist, temos como resultado a inversão do sentido da extrusão linear. Por hoje é isso, agora é com você, quais inovações utilizando a extrusão linear você pode incrementar em seus projetos de modelamento? Deixe nos comentários abaixo e até a próxima!